Fibonacciho posloupnost je nekonečná řada čísel, kterou popsal italský matematik Leonardo Pisánský zvaný Fibonacci již kolem roku 1 200. Podrobnosti o jejím využití lze najít např.zde
Pro podporu samostatné práce jsme vytvořili pracovní list: Fibonacci pracovní list
Výchozí úloha vede žáky k pochopení pravidla, podle kterého jsou řady čísel sestaveny. Pak žáci s řadami experimentují: mění výchozí čísla řady a sledují, jaký vliv to má na poslední číslo v řadě. Pak ve vytvořených řadách hledají pravidelnosti a formulují je. V závěru pracovního listu jsou vyzváni, aby odůvodnili závěry, ke kterým došli.
Pracovní list je podporou pro samostatné bádání žáků. Může být také využit při bádání strukturovaném.
Cílem řešení sekvence úloh je nalézt pravidelnost v datech, popsat ji a odůvodnit, proč k ní dochází.
Řady čísel, se kterými budeme pracovat, jsou vytvořeny podle podobného pravidla jako Fibonacciho posloupnost.
Cílem řešení první úlohy je, aby žáci pochopili, jak jsou řady čísel, se kterými budou dále pracovat, sestaveny.
Experimentování s čísly bývá v matematice často výchozí fází bádání. Žáci získávají data, jejichž porovnávání je vede k formulování pravidelností.
Úkol:
Experimentování s čísly pokračuje. Žáci si mají vyzkoušet, zda předchozí pozorování platí i pro druhé volené číslo.
Úkol:
Můžeme si také vyzkoušet, co se stane, když zaměníme pořadí zvolených čísel. V úloze 2. a 3. jsme již získali nějaké výsledky. Zde si vyzkoušíme, co se změní, když první dvě čísla řady vyměníme.
Úkol:
V závěru pracovního listu mají žáci shrnout své bádání a odpovědět na dvě otázky:
Jak se mění páté číslo, když změníme první a druhé číslo?
Proč to tak je?
Odpověď na první otázku je shrnutím toho, co žáci pozorovali při řešení předchozích úloh.
Druhá otázka směruje žáky ke zobecnění jejich pozorování. Odůvodnit, co se v číselné řadě děje je obtížné. Mohlo by pomoci obecnější vyjádření pomocí obrázků. Žák vidí, že třetí číslo je součtem prvních dvou. Čtvrté číslo je součtem prvního a dvojnásobku druhého čísla. Páté číslo je součtem dvojnásobku prvního čísla a trojnásobku druhého. To vysvětluje i naše pozorování při řešení úloh 2.- 4.
Číselné řady můžeme využít na zkoumání lichých a sudých čísel.
Při uvažování se žáci mohou opírat o znázornění čísla pomocí dvoukorun a koruny. Pro znázornění sudých čísel potřebujeme jen dvoukoruny. Pro znázornění lichých čísel potřebujeme kromě dvoukorun i jednu korunu. Pomocí tohoto znázornění žák pochopí, že součet dvou lichých čísel je vždy sudé číslo. Lichý součet mají jen dvojice čísel různé parity.
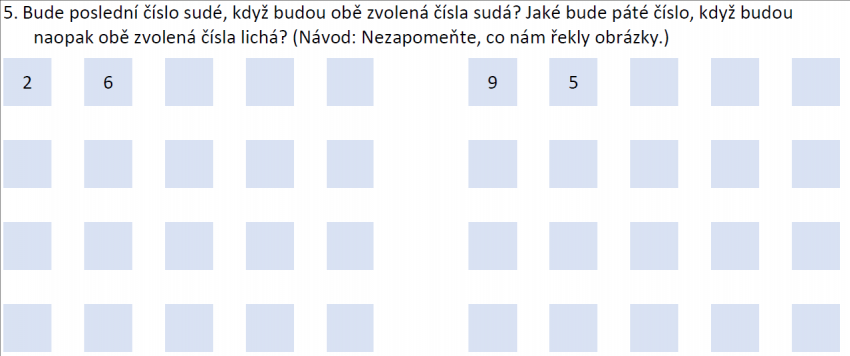
Číselné řady můžeme využít na zkoumání lichých a sudých čísel.
Úlohu mohou žáci řešit pokusem omylem. Mohou se opřít o to, co objevili při předchozím bádání.
Úkol:
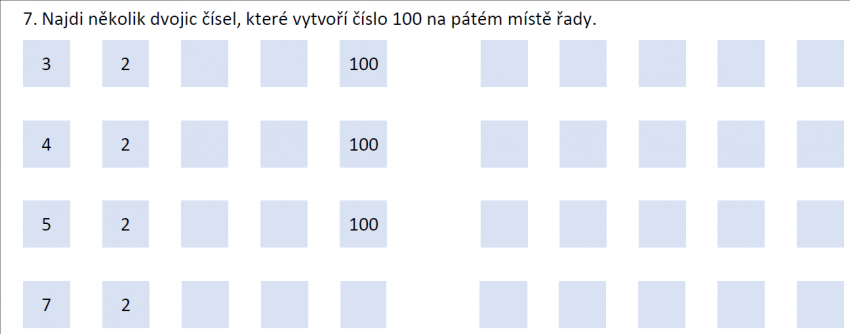
Metodou, která pomáhá žákům k hlubšímu porozumění, je tvoření úloh.
Zde mohou žáci např. vytvořit úlohy o řadách dlouhých 6 čísel. Mohou se ptát, co se stane, když na začátku řady (a) budou dvě stejná čísla, (b) zvolíme čísla jejichž rozdíl je 1, 2, 3, …, (c) je 0, apod.
Obsah