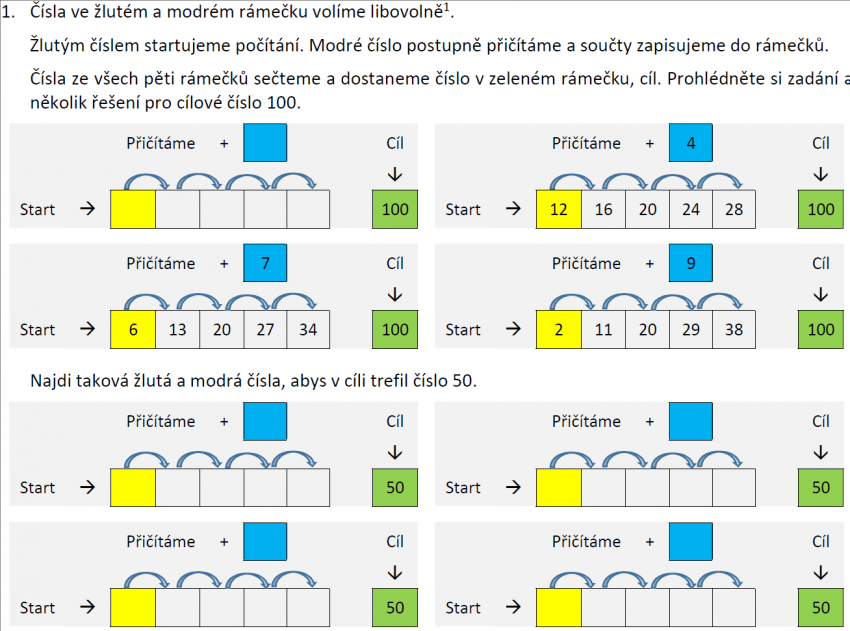
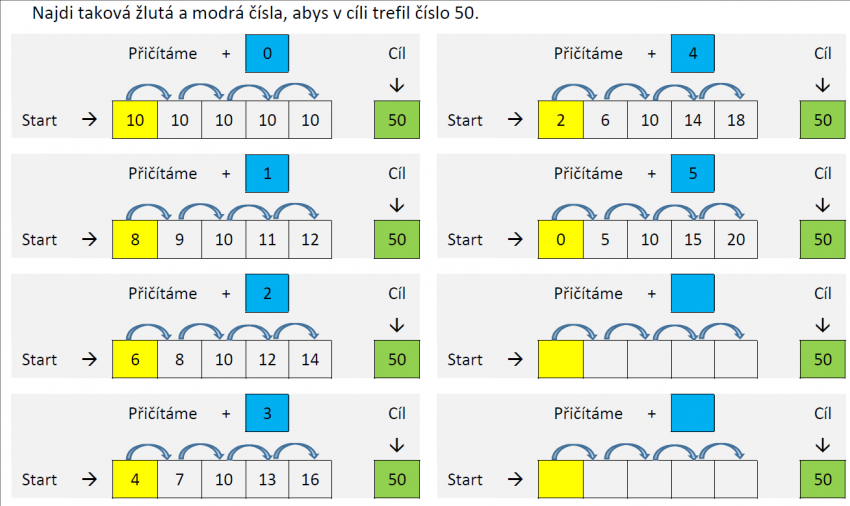
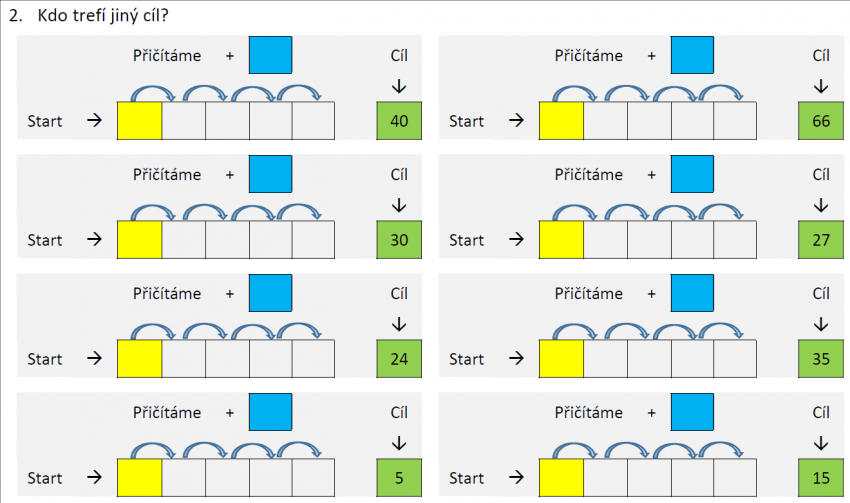
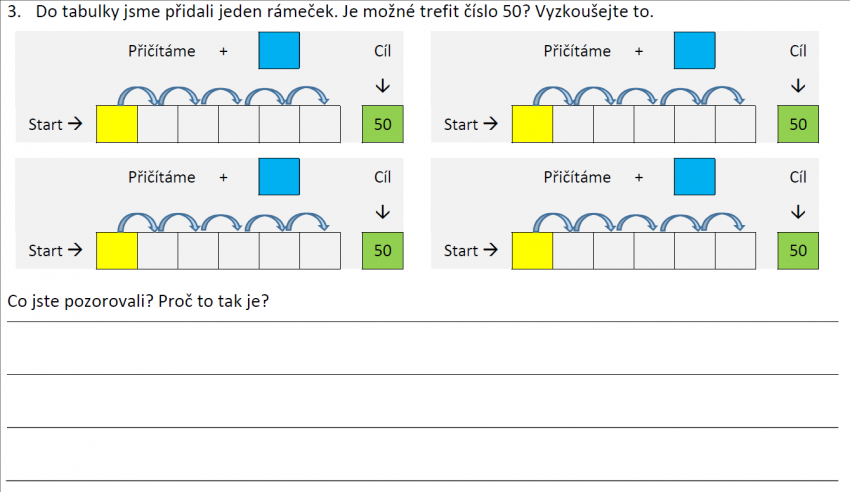
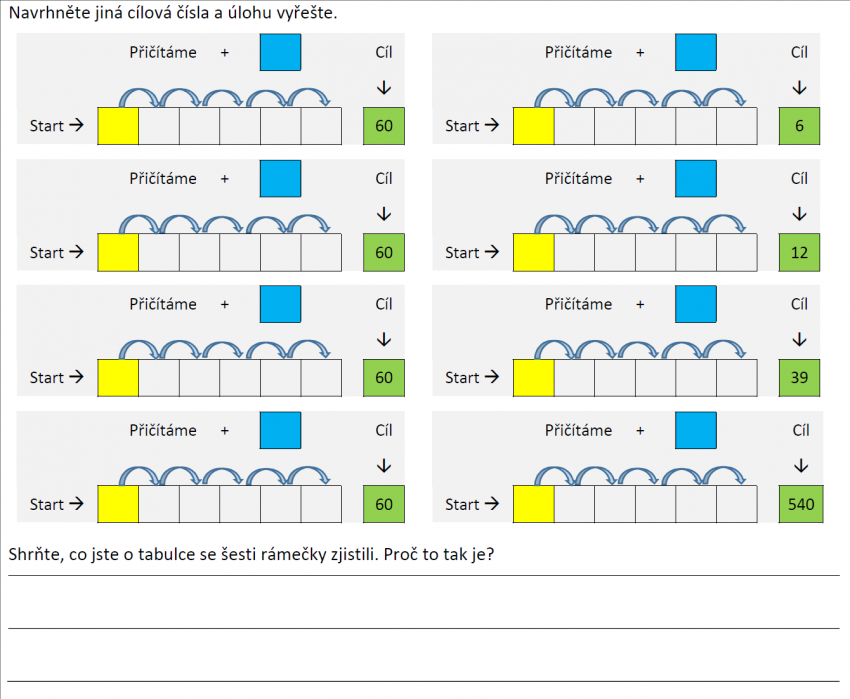
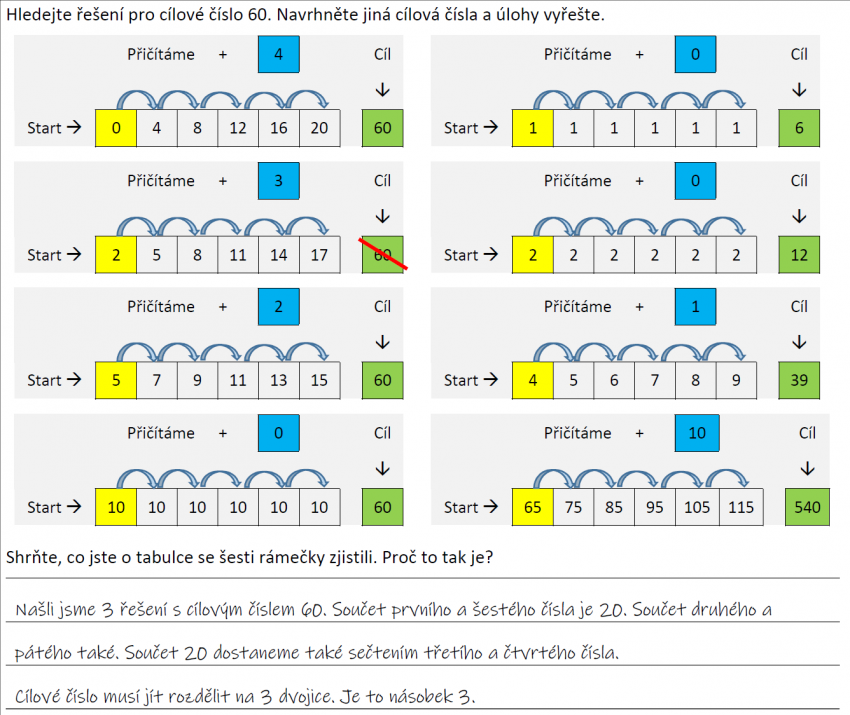
Úloha „Kdo trefí 50“ je jedním z námětů pro samostatné bádání žáků v aritmetice. Pro podnícení samostatné aktivity žáků jsme připravili pracovní list, který pomáhá žáky provést badatelským cyklem. Svým způsobem pracovní list přebírá za žáka odpovědnost za plánování experimentování s čísly.