Součtové pyramidy

Doprovodné materiály Informace o videu

Badatelsky orientovaná výuka

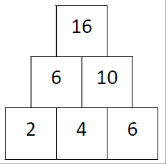
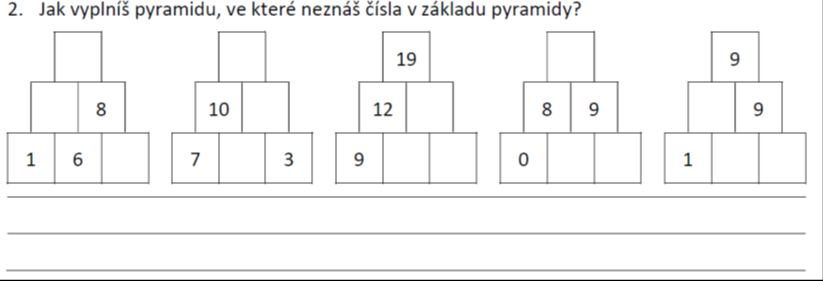
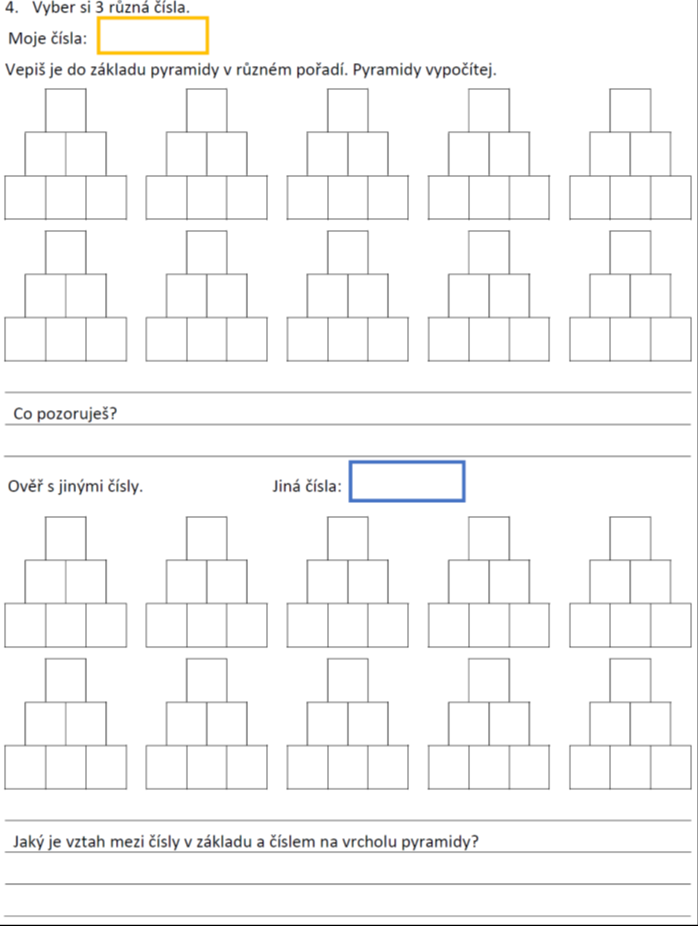
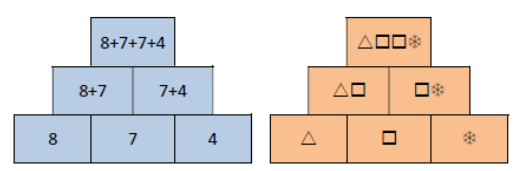
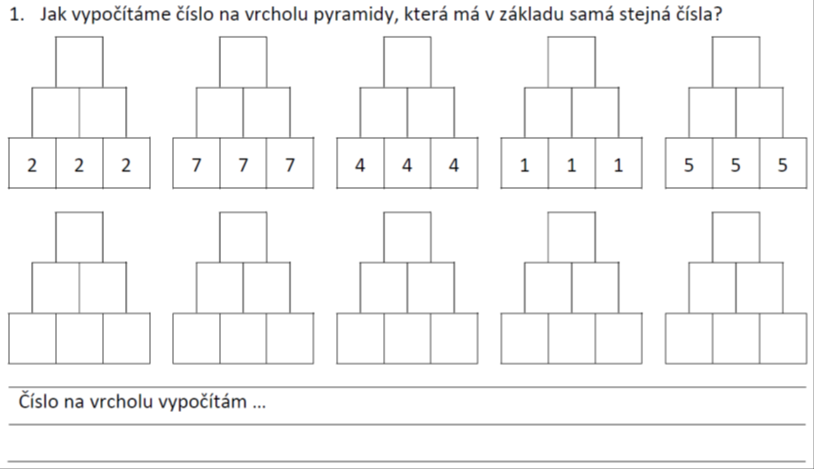
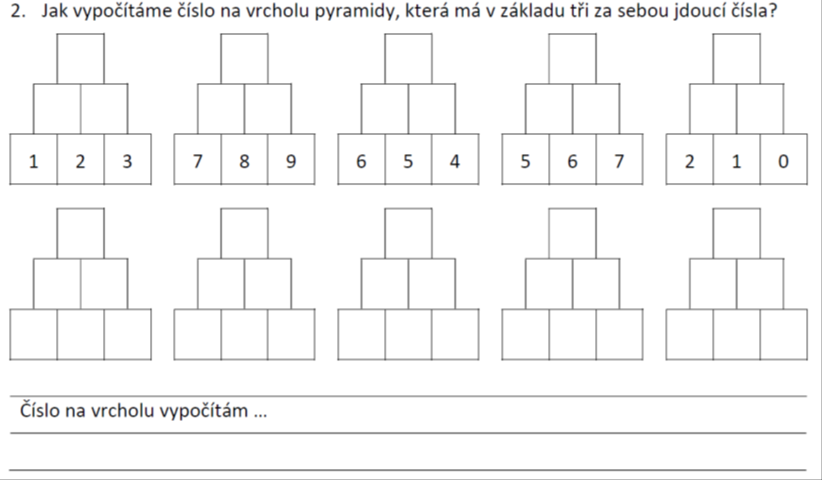
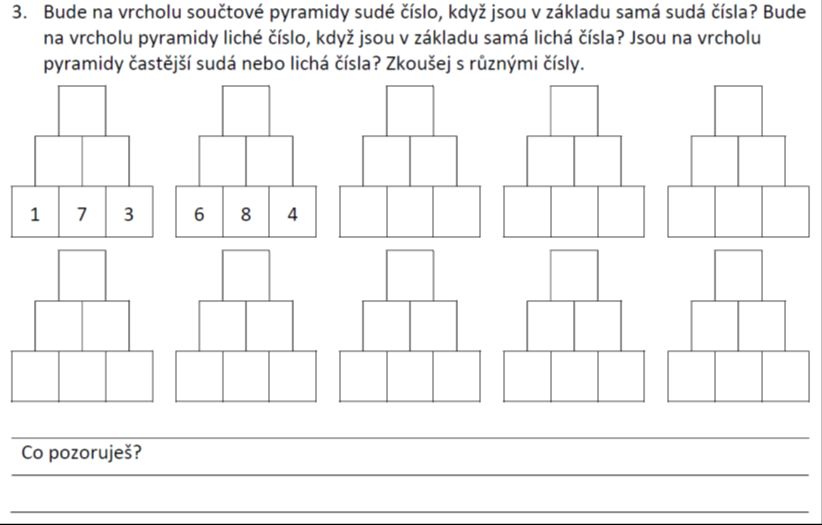
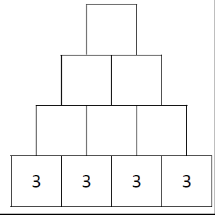
Badatelsky orientovaná výuka je jednou z aktivizujících metod. Učitel vhodnými úlohami podněcuje žáky k tomu, aby samostatně objevovali vlastnosti a vztahy matematických pojmů a struktur. Předpokládáme, že tak dojde k prohloubení porozumění.

Jak bádání žáků obvykle probíhá, znázorňuje schéma badatelského cyklu. Šipky ve schématu naznačují možné cesty bádání žáků. V případě potřeby může učitel bádání žáků usměrnit otázkami.

Více na Co je badatelsky orientovaná výuka matematiky (BOVM)

Součtové pyramidy

Součtové pyramidy jsou učebním prostředím, ve kterém můžeme tvořit úlohy nejen na procvičování pamětného sčítání a odčítání, ale také na prohloubení porozumění operacím sčítání a odčítání.

Sady úloh v tomto prostředí jsou na různých webech, které přinášejí úlohy motivující žáky k přemýšlení. V Hejného matematice nalezneme podobné prostředí nazvané Součtové trojúhelníky.

Sekvence následujících úloh je sestavena tak, aby mohli žáci samostatné objevovat souvislosti, které platí mezi čísly v součtové pyramidě.

Pro samostatnou práci žáků, či skupin žáků je možné použít pracovní list.

PL součtové pyramidy 1
PL součtové pyramidy 1 řešení

Součtové pyramidy a badatelsky orientovaná výuka

Úlohy jsou sestaveny tak, aby pracovní list vedl žáka k samostatnému bádání. To bývá znázorněno třeba tímto schématem badatelského cyklu.

Šipky ve schématu naznačují možné cesty bádání žáků. V případě potřeby může učitel bádání žáků usměrnit otázkami.

Více na Co je badatelsky orientovaná výuka matematiky (BOVM)

Úloha 1

Cílem řešení úloh 1 a 2 v pracovním listu je pochopení toho, jak se pracuje v učebním prostředí Součtové pyramidy. Z pohledu badatelského cyklu můžeme považovat tuto fázi za získávání zkušeností, všímání si, uvažování.

Pozn.: Čísla v základu pyramid jsou volena tak, aby úlohu mohli řešit i žáci, kteří sčítají jen do 20.

Prázdné pyramidy necháme žákům vyplnit podle jejich vlastního rozhodnutí.

Úkol:

Ke kterým učebním cílům směřuje řešení úlohy 1?:

Prostý text:

Úloha 2

Úkol:

Ke kterým učebním cílům směřuje řešení úlohy 2?:

Prostý text:

Úloha 3

Na základě zkušeností, které žák nasbíral při řešení úloh 1 a 2, se může pokusit zformulovat hypotézu o vztazích v pyramidě.

Úkol:

Jakou odpověď žáků očekáváte?:

Prostý text:

Úloha 4

Pracovní list je koncipován tak, aby žáci získali soubor dat, o která se mohou opřít při hledání vztahu mezi čísly v pyramidě.

Zeptáme se žáků, jak by mohli své návrhy (hypotézy) formulované v úloze 3 ověřit. Navrhneme vyzkoušet, co se v pyramidě děje, když do základu pyramidy dáme trojici čísel a měníme jejich pořadí. Poté necháme žáky experimentovat se dvěma trojicemi čísel.

Úkol:

Jakou odpověď žáků byste považovali za správnou?:

Prostý text:

Formulace závěru bádání

Závěr vycházející ze sčítání konkrétních čísel, můžeme doplnit obecnější úvahou.

Pokud si součty rozepíšeme (modrá pyramida), případně čísla nahradíme obrázky (oranžová pyramida), vidíme, že formulovaný vztah bude platit v každé třípatrové pyramidě.

Proč řešit tuto úlohu?

Řešení úlohy by mělo vést k tomu, že žák lépe pochopí vztahy mezi částmi a celkem, které jsou základem pro statickou intepretaci operaci sčítání a k ní inverzního odčítání.

Obdélník znázorňuje spojení žluté části (která třeba reprezentuje číslo 3) a modré části (reprezentuje 7) v šedý celek. Můžeme jej intepretovat jako znázornění sčítání (3 + 8 = 11), ale také dvou inverzních operací očítání: 11 – 3 a 11 – 8.

3	8
11

Analýza struktury vzdělávacího obsahu metodikou 3A

Úlohu můžeme rozebrat metodikou 3A. Více o teoretických východiscích analýzy struktury vzdělávacího obsahu naleznete v textu Metodika 3A.

Rozbor učebního prostředí metodikou 3A naleznete zde: Součtové pyramidy metodikou 3A

Je možné o součtových pyramidách objevit ještě něco?

Zadání úlohy 4 lze modifikovat a vytvářet tak podněty pro další bádání žáků. Některé náměty najdete ve formě úloh v pracovním listu níže.

Součtové pyramidy 2
PL součtové pyramidy 2 řešení

Úloha 1 (PL 2)

Žák si vyzkouší vypočítat několik pyramid. Podle zadání také sám volí čísla v základu.

Úkol:

Které pojmy byste zařadil(a) do konceptové vrstvy úlohy?:

Prostý text:

Úloha 2 (PL 2)

Bádání o pyramidách tohoto typu navazuje na závěry, ke kterým žák dospěl v úloze 1 PL pyramidy 2.

Úkol:

Jakou odpověď žáků byste očekával(a)?:

Prostý text:

Úloha 3 (PL 2)

Na řešení první úlohy také navazuje úloha, ve které se zaměřujeme na paritu čísel v základu a na vrcholu pyramidy.

Úkol:

Jaké názorné prostředky byste nabídl(a) žákům pro podporu řešení úlohy?:

Prostý text:

Úloha 4 (PL 2)

Hledání pyramid s určeným číslem na vrcholu může být projektem pro celou třídu.

Úkol:

S jakým cílem byste se žáky řešil(a) tuto úlohu?:

Prostý text:

Úloha 5 (PL 2)

Nabízí se i uvažování o vztazích v pyramidách s jiným počtem pater. Vzhledem k tomu, že žáci již mají mnoho zkušeností s bádáním v učebním prostředí, můžeme uvažovat o samostatném bádání žáků/skupin žáků. Úloha je vhodná i pro samostatnou práci talentovaného žáka.

Úkol:

Co když bude mít pyramida čtyři patra? Jaký je vztah mezi číslem na vrcholu pyramidy a čísly v základu?:

Prostý text:

Úloha 6 (PL 2)

Doporučujeme nechat úlohu řešit žáky samostatně. Pokud se podaří žákovi srozumitelně zformulovat závěr, prokazuje, že pochopil dobře učební prostředí a je schopen samostatně objevit některé aritmetické vztahy. Také žák prokazuje dobré pochopení sčítání a násobení.

Na úplné ukončení sekvence úloh, můžeme zařadit diskuzi o tom, co všechno jsme o součtových pyramidách objevili. Diskuze bude mít funkci institucionalizace.

Úkol:

Úloha 7 (PL 2)

Úloha není badatelská. Bude ale zajímavé sledovat, jaké pyramidy považují žáci za „speciální“.

Úkol:

Obsah