Otevřené úlohy
Badatelské úlohy neboli úlohy vhodné k využití při badatelsky orientované výuce jsou obvykle tzv. otevřené úlohy. Tyto úlohy splňují aspoň jednu z následujících charakteristik:
V tomto textu se tak budeme podrobně věnovat jedné matematické otevřené úloze a představíme si různé způsoby, jak je možné na ni pohlížet.
Úloha o zahradě a plotu
Mezi otevřené úlohy patří následující slovní úloha:
„Pan Plánička si koupil 12 plotových dílců a chce s nimi oplotit co největší část své obdélníkové zahrady, aby získal výběh pro slepice. Výběh by měl mít tvar čtverce nebo obdélníku. Jaké rozměry výběhu má zvolit?“
Úkol pro uživatele: Zkuste si úlohu vyřešit
Rozbor úlohy – 1. část
Protože v úloze není uveden žádný konkrétní rozměr plotových dílců, je vhodné stanovit si šířku jednoho plotového dílce jako jednotku délky a čtverec s takto dlouhou stranou jako jednotku obsahu (jednotkový čtverec).
Pokud bude pan Plánička ohrazovat volné prostranství uvnitř své zahrady, má tři možnosti, jak plotové dílce rozložit: do čtverce o rozměru 3 dílce x 3 dílce, do obdélníku o rozměru 2 dílce x 4 dílce, nebo do obdélníku o rozměru 1 dílec x 5 dílců.
Takový čtvercový výběh má plochu 9 jednotkových čtverců, první obdélníkový 8 jednotkových čtverců a druhý obdélníkový 5 jednotkových čtverců. Největší plochu z nich má čtvercový výběh.
Rozbor úlohy – 2. část
Pan Plánička však také při vytyčování svého výběhu může využít zeď nebo stávající plot ohraničující celou zahradu, pokud nějaké má. Využít je může jako ohraničení jedné, dvou, nebo dokonce tří stran výběhu.
Pokud je bude pan Plánička využívat na jednu stranu výběhu, má pět možnosti, jak plotové dílce rozložit:
do čtverce o rozměru 4 dílce x 4 dílce (s obsahem 16),
do obdélníku o rozměru 5 dílců x 2 dílce (s obsahem 10),
do obdélníku o rozměru 3 dílce x 6 dílců (s obsahem 18),
do obdélníku o rozměru 2 dílce x 8 dílců (s obsahem 16),
nebo do obdélníku o rozměru 1 dílec x 10 dílců (s obsahem 10).
Největší plochu z nich má obdélníkový výběh 3 x 6.
Rozbor úlohy – 3. část
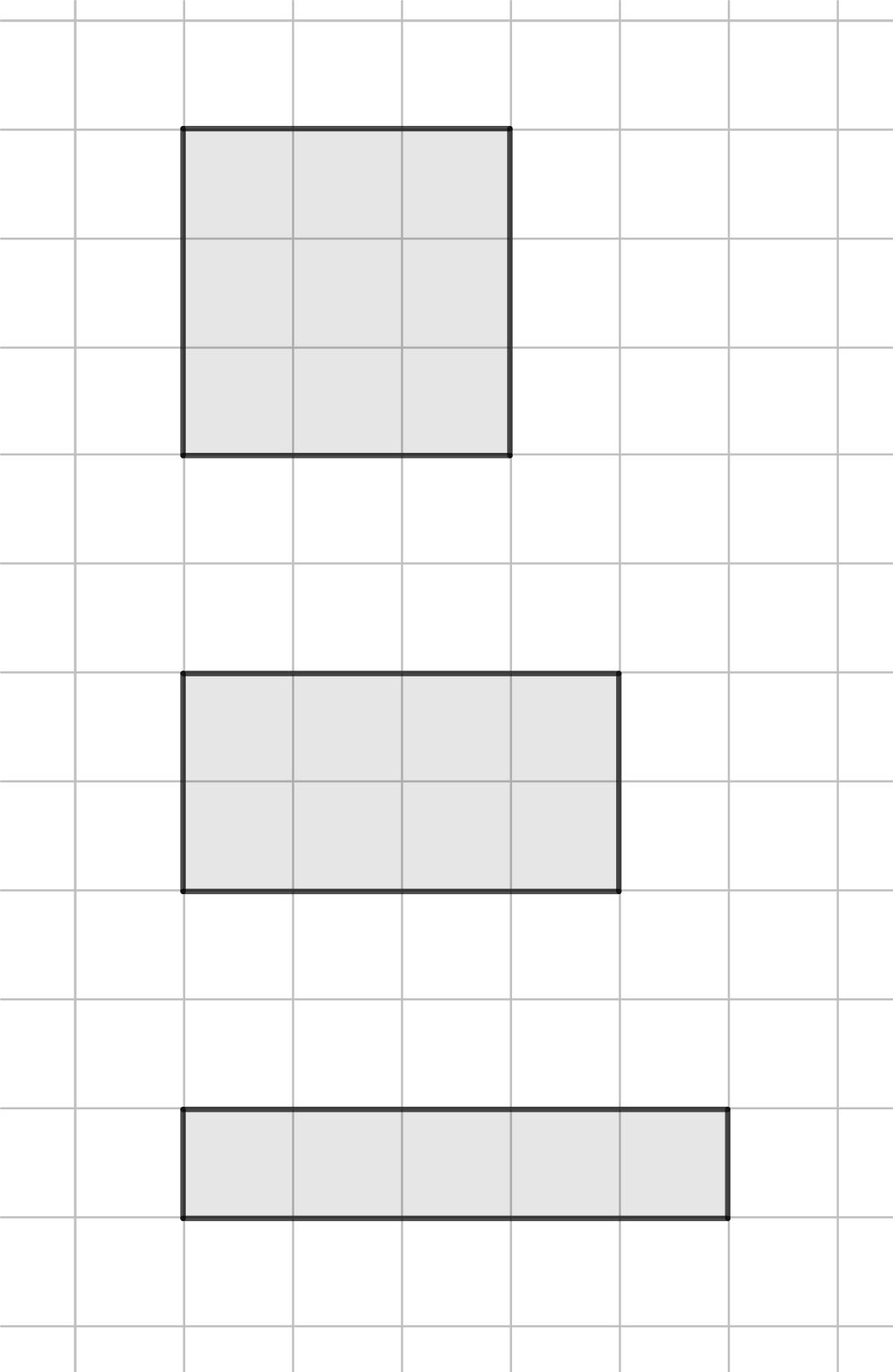
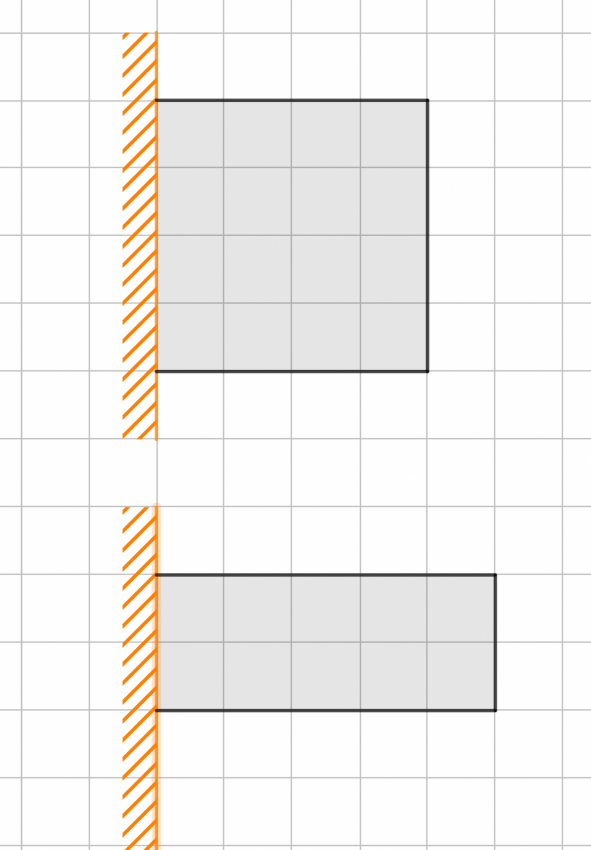
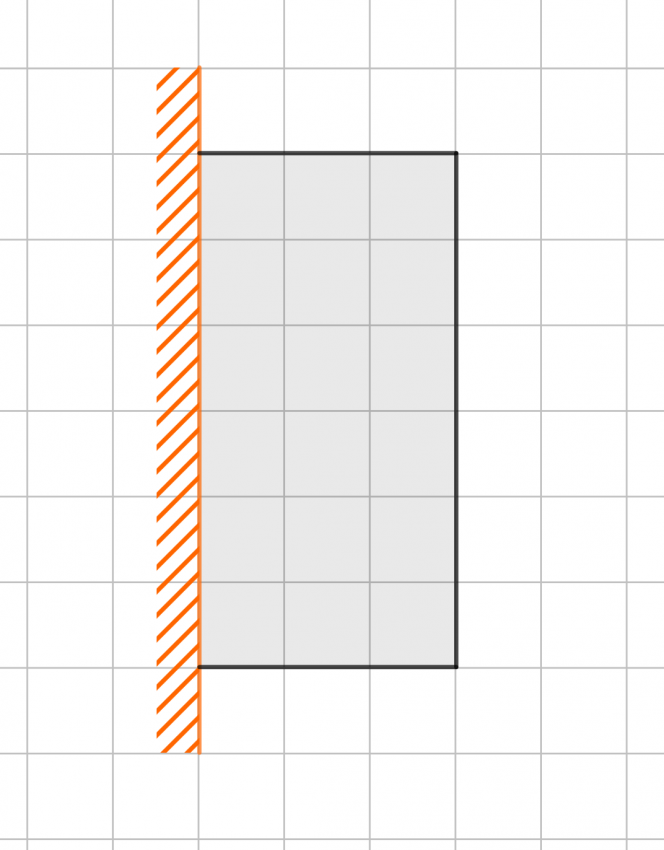
Pokud je bude pan Plánička využívat zeď nebo starý plot na ohraničení dvou stran výběhu, tak má šest možnosti, jak plotové dílce rozložit.
Úkol
*TODO: v odpovědi nelze zatím použít obrázky
Jak úlohu řešit s žáky
Úloha o plotu kolem slepičího výběhu pana Pláničky má mnoho řešení, která závisejí mj. i na tom, jaké rozměry má celá zahrada, jestli má kolem sebe plot nebo zeď, kde přesně chce pan Plánička slepičí výběh v zahradě umístit. Žádná z těchto informací není uvedena v zadání úlohy.
Taková situace je obvyklá u prakticky založených úloh a způsobuje, že úlohu není možné celou kompletně vyřešit. Výhodou je, že pak taková úloha nabízí mnoho prostoru pro bádání žáků.
Prakticky založené úlohy s sebou také někdy přinášejí jistou nejednoznačnost či neurčitost terminologickou, neboť jejich kontext není čistě matematickým kontextem. Tato neurčitost pak hraje svou roli při matematizaci úlohy. V naší úloze ji může navodit otázka, co to vlastně znamená „největší výběh“, jaká měřitelná vlastnost geometrického útvaru jeho velikost určuje.
Žáky můžeme rozdělit do malých skupinek, nechat je bádat, a potom skupinky jednu po druhé vyzvat k představení svého/svých řešení. Bádání žáků v takovém případě postupuje podle schématu badatelského cyklu. Více o tom, jak se v takovém schématu vyznat, naleznete na Hyperspace v menu Úlohy pod názvem „Jak se vyznat v badatelském cyklu“.
Shrnutí
Představili jsme si prakticky založenou badatelskou úlohu s geometrickou matematizací, její různá řešení a způsob, jak je možné ji řešit a diskutovat s žáky. Úloha se vztahuje k tématu obsah pravoúhelníku ve čtvercové síti, je tedy vhodná pro žáky prvního i druhého stupně základní školy. Okrajově je řešen vztah obsahu a obvodu, a také praktické aplikace tématu maximální obsah při pevně daném obvodu.
Níže uvedená literatura se týká badatelských úloh jako takových (Samková a kol., 2015) a dalších možností, jak je možné s žáky badatelsky zkoumat obsah libovolných geometrických útvarů při pevně daném obvodu (Samková, 2017).
Literatura
Samková, L. (2017) Badatelské úlohy ve vyučování matematice. Sborník 8. konference Užití počítačů ve výuce matematiky, str. 116-131. Č. Budějovice: Jihočeská univerzita. Dostupné zde
Samková, L., Hošpesová, A., Roubíček, F., Tichá, M. (2015) Badatelsky orientované vyučování matematice. Scientia in educatione, 6(1), 91-122. Dostupné na https://ojs.cuni.cz/scied/article/download/154/145/0
Obrázek plotu: https://www.freepik.com/free-vector/wooden-fence-tile_1529606.htm
Obrázek slepice: https://www.freepik.com/free-vector/silhouette-color-outline-version-chickens_5837306.htm