Schéma výukového bloku s badatelskou úlohou
Při plné implementaci badatelsky orientovaného vyučování se každá výuková jednotka skládá ze čtyř kroků tak, jak je uvedeno vedle na obrázku 1, a blok s evokací předchází řešení vybrané badatelské úlohy. Při evokaci tak učitel ověřuje aktuální stav těch znalostí žáků, které budou nezbytné pro řešení badatelské úlohy (znalostí, bez kterých není možné badatelskou úlohu úspěšně vyřešit). Pokud učitel během evokace zjistí výrazné nedostatky ve znalostech, může se rozhodnout, že realizaci badatelské úlohy odloží.

Pokračovat
Schéma evokace
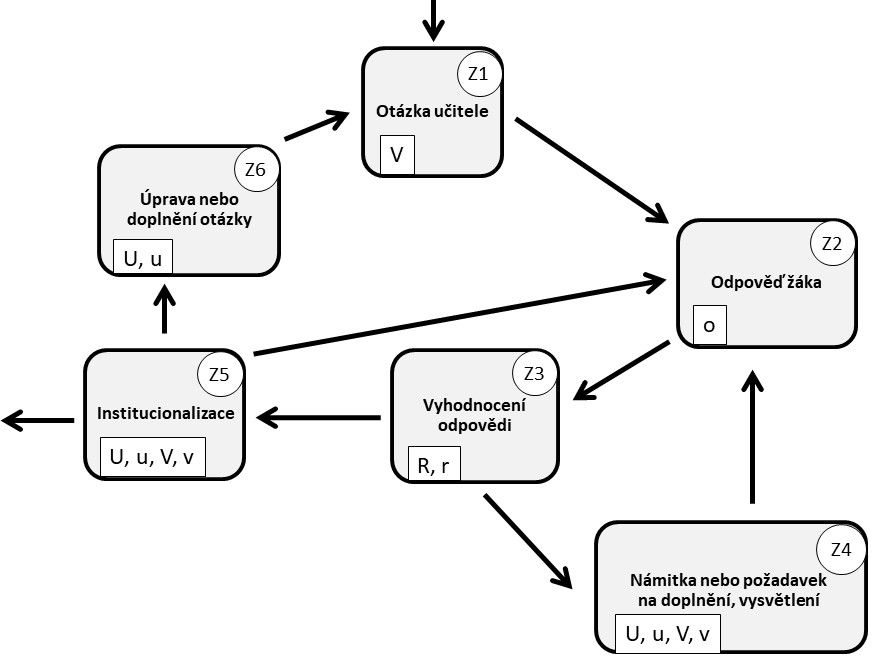
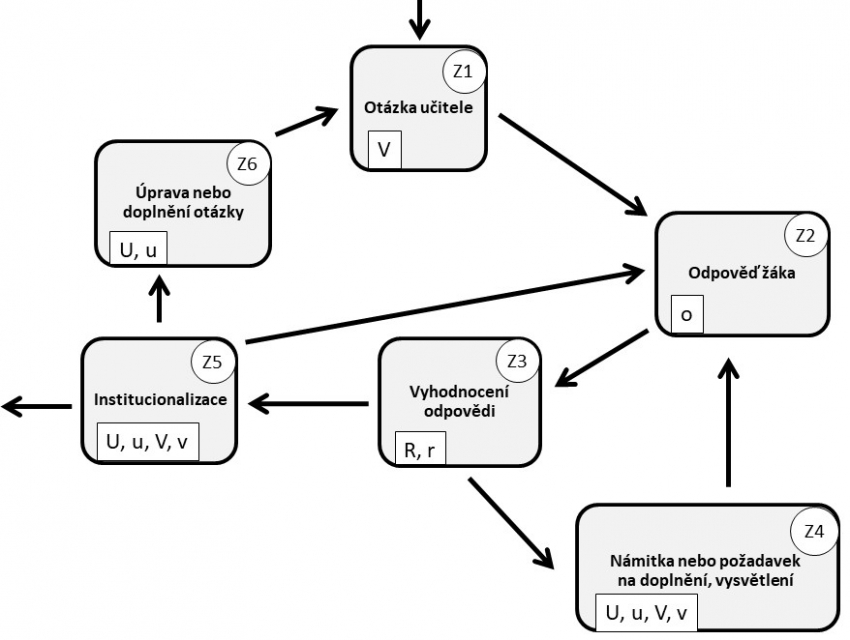
V ideálním případě má evokace podobu diskuse, jejíž průběh znázorňuje schéma na obrázku 2. Průchod schématem začíná nahoře uprostřed (dlaždicí "Otázka učitele") a končí vlevo dole (dlaždicí "Institucionalizace"), možné cesty mezi dlaždicemi naznačují šipky.
Pokračovat
Evokace z pohledu badatelského cyklu
Činnosti badatelského cyklu, ke kterým se jednotlivé dlaždice z obrázku 2 vztahují, jsou specifikovány nápisem na dlaždici. Dlaždice s nápisem "Institucionalizace" odkazuje na průběžné nebo závěrečné shrnutí dosavadních zjištění diskuse (co už víme, co ještě není jasné, co platí, co neplatí, jak bychom to mohli dál využít, co by nás ještě zajímalo apod.). Každá dlaždice má v kolečku v pravém horním rohu svou značku, kterou budeme v dalším textu používat pro zápis průchodu schématem.
Cesty mezi dlaždicemi naznačují šipky. U některých dlaždic je možná jen jedna cesta dál, například po dlaždici "Odpověď žáka" musí vždy následovat dlaždice "Vyhodnocení odpovědi". U některých dlaždic je možných dalších cest více, po dlaždici "Vyhodnocení odpovědi" může následovat buď dlaždice "Námitka nebo požadavek na doplnění, vysvětlení", nebo dlaždice "Institucionalizace". Nejkratší průchod schématem tak může například odpovídat situaci, kdy učitel položí otázku, žák na ni odpoví, učitel odpověď vyhodnotí jako správnou a na jejím základě vše shrne; takový průchod schématem bychom pomocí značek zapsali jako Z1 – Z2 – Z3 – Z5. V praxi však evokace obsahuje více než jen jednu otázku a jednu odpověď, učitel může například opakovaně vyžadovat doplnění nebo vysvětlení žákovy odpovědi, takže se několikrát zopakuje smyčka Z2 – Z3 – Z4 – Z2.

Pokračovat
Shrnutí
Na několika virtuálních záznamech výukových dialogů (tabulky 1 až 6) jsme si představili možnosti praktického využití schématu evokace (obrázek 2) pro lepší orientaci v jevech, které souvisejí s badatelským cyklem (tabulky 1 až 3) a s formativním hodnocením (tabulky 4 až 6). Tímto způsobem je možné posuzovat a analyzovat již realizovanou výuku, ale také je možné s pomocí schématu výuku připravovat. Výskyt jednotlivých kódových písmen formativního hodnocení, jejich velikost a jejich frekvence umožňují přehledné charakteristiky realizované diskuse, jak ukázalo porovnání diskusí z tabulek 4, 5 a 6. Pro správné badatelsky orientované vyučování a formativní hodnocení je nezbytný výskyt kódů R, r, U, u; pro vrstevnické hodnocení výskyt kódů r, u, v.
Jak již bylo řečeno v úvodu, evokaci je možné považovat za jakýsi předstupeň plně badatelsky orientované výuky. Je možné ji realizovat samostatně, bez vazby na řešení badatelské úlohy, a tak si nacvičovat vedení badatelsky orientované diskuse učitele a žáků. Pro samotnou realizaci badatelské úlohy (třetí dlaždice na obrázku 1) existuje podobné schéma, jako je schéma evokace z obrázku 2, ale toto schéma je větší, komplikovanější a má několik úrovní. Více informací lze nalézt v sekci Jak se vyznat v badatelském cyklu
Literatura
Rokos, L., & Samková, L. (2020). Coding classroom talk from the perspective of formative assessment and inquiry-based education: a communication model for mathematics and science lessons. Proceedings of ICERI 2020 conference (1170–179).
Samková, L., Rokos, L., Petr, J., & Stuchlíková, I. (2021) Teoretický model pro formativní hodnocení při badatelsky orientované výuce matematiky a přírodopisu. Pedagogika. 71(1), 29–56. https://doi.org/10.14712/23362189.2020.1836